Perceptron

Perceptron

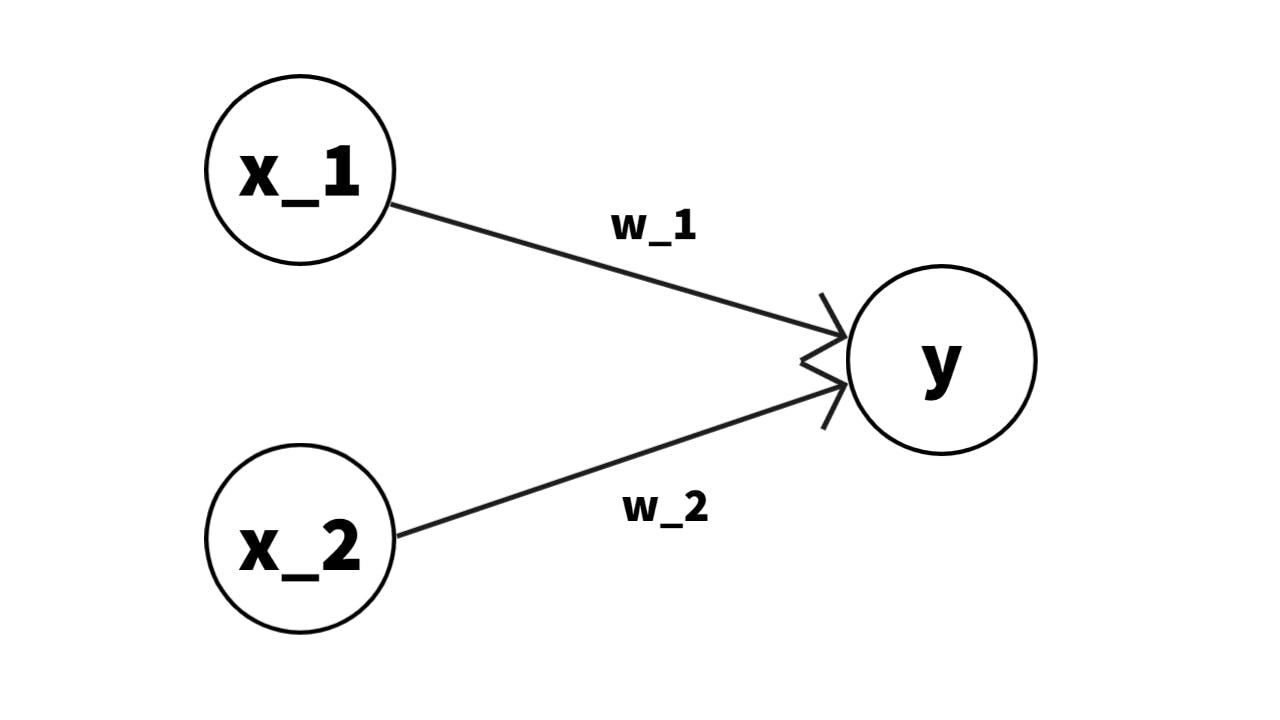
Perceptron, the foundation algorithm for deep learning, came up by Frank Rosenblatt in 1957. Perceptrons receive multiple signals and output one signal, the signal is only two values, which are 0 or 1. Perceptron has weight, the signal is important relation to the dependence of weight.

In the example above, w_1 and w_2 are called weight, and b is called bias. By manipulating the weight and bias, people can control output.

Simple Example of Perceptron

1. AND Gate

AND gate only outputs 1 when both inputs are 1.

x_1 (input 1)	x_1 (input 2)	y (output)
0	0	0
1	0	0
0	1	0
1	1	1

def AND(x1, x2):
  x = np.array([x1, x2])
  w = np.array([0.5, 0.5])
  b = -0.7 # b is bias
  return 0 if np.sum(w*x) + b <= 0 else 1

print(AND(1, 1)) # 1
print(AND(1, 0)) # 0
print(AND(0, 1)) # 0
print(AND(0, 0)) # 0

2. OR Gate

OR gate outputs 1 when either input or both outputs are 1.

x_1 (input 1)	x_1 (input 2)	y (output)
0	0	0
1	0	1
0	1	1
1	1	1

def OR(x1, x2):
  x = np.array([x1, x2])
  w = np.array([0.5, 0.5])
  b = -0.2
  return 0 if np.sum(w*x) + b <= 0 else 1

print(OR(1, 1)) # 1
print(OR(1, 0)) # 1
print(OR(0, 1)) # 1
print(OR(0, 0)) # 0

3. NAND Gate

NAND gate does not output 1 when both of the inputs are 1.

x_1 (input 1)	x_1 (input 2)	y (output)
0	0	1
1	0	1
0	1	1
1	1	0

def NAND(x1, x2):
  x = np.array([x1, x2])
  w = np.array([-0.5, -0.5])
  b = 0.7
  return 0 if np.sum(w*x) + b <= 0 else 1

print(NAND(1, 1)) # 0
print(NAND(1, 0)) # 1
print(NAND(0, 1)) # 1
print(NAND(0, 0)) # 1

4. XOR gate

XOR gate outputs 1 only when either input is 1. Unlike AND, OR, and NAND gates, the XOR gate is not linear. Thus, it is impossible to code the XOR gate only using NumPy matrix. By using NAND, AND, and OR gates, the XOR gate can be implemented. Also, using multiple perceptrons to create the other perceptron is called multi-layered perceptron.

x_1 (input 1)	x_1 (input 2)	y (output)
0	0	0
1	0	1
0	1	1
1	1	0

def XOR(x1, x2):
  s1 = NAND(x1, x2)
  s2 = OR(x1, x2)
  return AND(s1, s2)

print(XOR(1, 1)) # 0
print(XOR(1, 0)) # 1
print(XOR(0, 1)) # 1
print(XOR(0, 0)) # 0